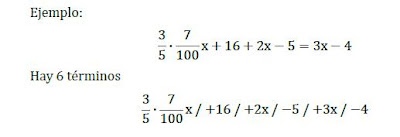ISAAC NEWTON (1642-1727):

 Newton, Isaac (1642-1727), matemático y físico británico, considerado uno de los más grandes científicos de la historia, que hizo importantes aportaciones en muchos campos de la ciencia. Sus descubrimientos y teorías sirvieron de base a la mayor parte de los avances científicos desarrollados desde su época. Newton fue junto al matemático alemán Gottfried Wilhelm Leibniz uno de los inventores de la rama de las matemáticas denominada cálculo. También resolvió cuestiones relativas a la luz y la óptica, formuló las leyes del movimiento y dedujo a partir de ellas la ley de la gravitación universal

Algunos problemas

Agrupamos los términos semejantes y los independientes, y sumamos:

     

   

Quitamos paréntesis:

Agrupamos términos y sumamos:

Despejamos la incógnita:

 

 

Quitamos denominadores, para ello en primer lugar hallamos el mínimo común múltiplo.

Quitamos paréntesis, agrupamos y sumamos los términos semejantes:

Despejamos la incógnita:

        

Quitamos paréntesis y simplificamos:

Quitamos denominadores, agrupamos y sumamos los términos semejantes:

  

  

Resolver

1 Un padre tiene 35 años y su hijo 5. ¿Al cabo de cuántos años será la edad del padre tres veces mayor que la edad del hijo? 

2Si al doble de un número se le resta su mitad resulta 54. ¿Cuál es el número?

3 La base de un rectángulo es doble que su altura. ¿Cuáles son sus dimensiones si el perímetro mide 30 cm?

4En una reunión hay doble número de mujeres que de hombres y triple número de niños que de hombres y mujeres juntos. ¿Cuántos hombres, mujeres y niños hay si la reunión la componen 96 personas? 

5 Se han consumido 7/8 de un bidón de aceite. Reponemos 38 l y el bidón ha quedado lleno hasta sus 3/5 partes. Calcula la capacidad del bidón.

6 Una granja tiene cerdos y pavos, en total hay 35 cabezas y 116 patas. ¿Cuántos cerdos y pavos hay?

7Luís hizo un viaje en el coche, en el cual consumió 20 l de gasolina. El trayecto lo hizo en dos etapas: en la primera, consumió 2/3 de la gasolina que tenía el depósito y en la segunda etapa, la mitad de la gasolina que le queda. Se pide:

1.Litros de gasolina que tenía en el depósito.

2. Litros consumidos en cada etapa.

8En una librería, Ana compra un libro con la tercera parte de su dinero y un cómic con las dos terceras partes de lo que le quedaba. Al salir de la librería tenía 12 €. ¿Cuánto dinero tenía Ana?

9 La dos cifras de un número son consecutivas. La mayor es la de las decenas y la menor la de las unidades. El número es igual a seis veces la suma de las cifras. ¿Cuál es el número?

 

10Las tres cuartas partes de la edad del padre de Juan excede en 15 años a la edad de éste. Hace cuatro años la edad de la padre era doble de la edad del hijo. Hallar las edades de ambos.

11Trabajando juntos, dos obreros tardan en hacer un trabajo 14 horas. ¿Cuánto tiempo tardarán en hacerlo por separado si uno es el doble de rápido que el otro?

12Halla el valor de los tres ángulos de un triángulo sabiendo que B mide 40° más que C y que A mide 40° más que B.

Repaso ( Conceptos)

Cualquier expresión que incluya la relación de igualdad (=) se llama ecuación.
Una ecuación se denomina identidad si la igualdad se cumple para cualquier valor de las variables; si la ecuación se cumple para ciertos valores de las variables pero no para otros, la ecuación es condicional.
Un término es una expresión algebraica que sólo contiene productos de constantes y variables; 2x, – a, 3s4x, x²(2zy)³ son algunos ejemplos de términos.
La parte numérica de un término se denomina coeficiente.
Los coeficientes de cada uno de los ejemplos anteriores son 2, –1, 3 y 8 (el último término equivale a x²{8(zy)³} y se puede escribir también como 8x²(zy)³.
Una expresión que contiene un solo término se denomina monomio, dos términos, binomio y tres términos, trinomio.
Un polinomio es una suma (o diferencia) finita de términos.
En este contexto, el grado es el mayor exponente de las variables en un polinomio.
Por ejemplo, si el mayor exponente de la variable es 3, como en ax³ + bx² + cx, el polinomio es de tercer grado.
Una ecuación lineal en una variable es una ecuación polinómica de primer grado; es decir, una ecuación de la forma ax + b = 0.
Se les llama ecuaciones lineales porque representan la fórmula de una línea recta en la geometría analítica.
Una ecuación cuadrática en una variable es una ecuación polinómica de segundo grado; es decir, de la forma ax² + bx + c = 0.
Un número primo es un entero (número natural) que sólo se puede dividir exactamente por sí mismo y por 1. Así, 2, 3, 5, 7, 11 y 13 son todos números primos.
Las potencias de un número se obtienen mediante sucesivas multiplicaciones del número por sí mismo.
El término a elevado a la tercera potencia, por ejemplo, se puede expresar como a·a·a o a³.
Los factores primos de un cierto número son aquellos factores en los que éste se puede descomponer de manera que el número se puede expresar sólo como el producto de números primos y sus potencias.
Por ejemplo, los factores primos de 15 son 3 y 5. Del mismo modo, como 60 = 2² × 3 × 5, los factores primos de 60 son 2, 3 y 5

Solucion de Ecuacion

 una ecuación es de primer grado cuando la variable (x) no está elevada a ninguna potencia, es decir, su exponente es 1. Una ecuación de primer grado tiene la forma canónica:

con a diferente de cero.
Su solución es la más sencilla:

Resolución de ecuaciones de primer grado

Dada la ecuación:

1- Transposición:
Primero, se agrupan los monomios que poseen la variable x en uno de los miembros de la ecuación; normalmente, en el izquierdo. Podemos hacerlo teniendo en cuenta que:

Si sumamos (o restamos) un mismo monomio (o número) en los dos miembros, la igualdad no varía.

En términos coloquiales, se suele decir: si el número está sumando (Ej: +9), pasa al otro lado restando (-9); y si el número está restando (Ej: -6), pasa al otro lado sumando (+6)
La ecuación quedará así:

Como puede verse, todos los términos que poseen la variable x han quedado en el primer miembro (a la izquierda del signo igual), y los que no la poseen, por ser sólo constantes numéricas, han quedado en el segundo miembro (a la derecha).
2- Simplificación:
El siguiente paso es convertir la ecuación en otra equivalente más simple y corta.
Realizamos la simplificación del primer miembro:
Y simplificamos el segundo miembro:
La ecuación simplificada será:

3- Despejar:
Ahora es cuando llegamos al objetivo final: que la variable quede en un término de la igualdad.

Si multiplicamos por un mismo monomio (o número) en los dos miembros, la igualdad no varía.

En términos coloquiales: si el número está multiplicando (Ej: ·2), pasa al otro lado dividiendo (en forma fraccionaria) (n/2) (el número pasará sin cambiar su signo).

Si dividimos entre un mismo monomio (o número) en los dos miembros, la igualdad no varía.

En términos coloquiales: si el número está dividiendo (expresado en forma fraccionaria) (Ej: n/5), pasa al otro lado multiplicando (·5) (el número pasará sin cambiar su signo).
Coloquialmente: en la ecuación, debemos pasar el número 95 al otro lado y, como está multiplicando, pasa dividiendo (sin cambiar de signo):

Se comprueba que el ejercicio está teóricamente resuelto, ya que tenemos una igualdad en la que x equivale al número 525/95. Sin embargo, debemos simplificar.
Resolvemos la fracción (numerador dividido entre denominador) en caso de que el resultado diera exacto; si diera decimal, simplificamos la fracción y ése es el resultado.
En la ecuación, vemos que el resultado de la fracción es decimal (525:95 = 5,5263157894737)
Por tanto, simplificando, la solución es:

Ecuacion

Es una expresión algebraica que consta de dos miembros separados por un signo de igualdad. Uno o ambos miembros de la ecuación debe tener al menos una variable o letra, llamada incógnita. Las ecuaciones se convierten en identidades sólo para determinados valores de la(s) incógnita(s). Estos valores particulares se llaman soluciones de la ecuación. Ejemplo:

La ecuación: 3X - 8 = 10 sólo se cumple para X = 6, ya que si sustituimos dicho valor en la ecuación quedará la identidad: 10 = 10. Por lo tanto decimos que X = 6 es la solución de la ecuación dada. De hecho, es la única solución. Si usáramos, por ejemplo, X = 2, resultaría -2 = 10 (un absurdo)

Resolver una ecuación es hallar los valores de X que la satisfacen a través de técnicas matemáticas variadas. Si la ecuación es de primer grado, un despeje es el procedimiento general. Si el grado de la ecuación es superior a uno, deben utilizarse otros métodos.

Valor Numerico de Una Expresion Algebraica

El valor numérico de una expresión algebraica es el valor (número) que adquiere
la expresión al sustituir la incógnita o incógnitas por su valor o valores.
Ejemplo: Hallar el valor numérico de 5x – 8 para x =5 y para x = 7

Ejemplo: Dada la expresión algebraica 5ax2 – 7x – 2a3. Hallar el valor numérico
cuando la incógnita x vale 10 y la incógnita a vale – 1

 

Suma Y Resta De Expresiones Algebraicas

Condiciones:

1. Solo se pueden sumar o restar términos semejantes; es decir a
aquellos que tienen la misma parte literal
.
B. Definición:
Para sumar o restar los términos semejantes, se suman o retan los
coeficientes y se conservan la parte literal elevada a la misma potencia.

– 2x2 + x – 15 + 19y2 + 2ab.
Sumar o restar términos semejantes también se llaman reducir términos
semejantes.

Expresiones Algebraicas

Concepto:
Una expresión algebraica es una combinación de números y letras unidos o
ligados por las operaciones aritméticas de:

 Suma.
 Resta.
 Multiplicación.
 División
.
B. Términos de una expresión algebraica:
Se llaman así a las expresiones numéricas o algebraicas separadas por los
signos de sumar o restar.

C. Tipos de Términos:
A. Términos en x
Son aquellos términos de la expresión que dependen del valor de la
incógnita (de la x).
Todos estos términos llevan incógnita. ( en el ejemplo anterior la incognita era X )

Términos Independientes.
Son aquellos términos de la expresión que no dependen del valor de
la incógnita (por eso se llaman independientes).
Tienen el valor numérico que representan.
En el ejemplo anterior son términos independientes +16 / 5 / 4

Partes de un término de una expresión algebraica.
A. Coeficiente:
Es la parte numérica, que generalmente se pone delante de la
incógnita o de las incógnitas.
B. Parte literal:
Se refiere a la letra o letras que hay en cada término de la expresión.
Ejemplo: En la expresión 3x + 5
3x→ es un término 3→ es el coeficiente x →es la parte literal

Observaciones:
1. El factor 1 o coeficiente 1 no se escribe 1x2y → x2y
2. El exponente 1 tampoco se pone 3x1y2 → 3xy2
3. El signo de multiplicar no suele ponerse ni entre las letras, ni entre
los números y las letras 5▪a▪b▪c3 →5abc3
Copia en tu cuaderno el apartado: Lectura correcta de expresiones algebraicas.
Ejercicios nº 2 y 3

F. Términos semejantes:
En una expresión algebraica los términos semejantes son aquellos que tiene
la misma parte literal (mismas incógnitas elevadas a los mismos
exponentes)
Ejemplo: Dada la expresión
5x – 7 + 10y2 = 4x – 8 + 9y2 – 3ab + 5ab – 2

Lenguaje Algebraico ( ejercicios)

  Ejercicios:

        A continuación te sugerimos realices el ejercicio, donde tienes que expresar en forma verbal o escrita los diferentes términos según sea el caso.

a)

b) El cociente de la suma de dos números sobre tres.

c) El cociente de la suma de dos números sobre 3 veces el primer sumando.

d) (x–4)c

e) La diferencia de los números es mayor que su cociente.

f) (3x)²

g) El triple del cuadrado de la diferencia de un binomio.

h)

i) La suma del doble de un número con otro número.

j) El cubo de la raíz cuadrada de la suma de dos número

Expresiones Algebraicas

Forma   verbal	Forma escrita		Forma verbal	Forma escrita
Suma	+		El triple de un número	3x
Diferencia	-		El cuádruplo de un número	4x
Producto	( ) ( ), . , ab		El quíntuplo de un número	5x
Cociente	/, ÷		El doble de la suma de dos números	2(a+b)
Raíz cuadrada			El triple de la diferencia de dos números	3(x-y)
Potencia	( )n dónde n , es cualquier número		La mitad de un número	X/2
Un número cualquiera	X		La mitad de la diferencia de dos números
La suma de dos números	A + b		La cuarta parte de un número	X/4
La resta o diferencia de dos números	X – y		El cuadrado de un número	X2
El producto de dos números	Ab		El cuadrado de la suma de dos números	(x + 4 ) 2
El cociente de dos números	X/y		El triple del cuadrado de la suma de dos números.	3(x+4)2
La raíz cuadrada de un número			La suma de 3 números	A+b+c
El cociente de la suma de dos números, sobre la diferencia			La semi suma de dos números.
El doble de un número	2x		El cubo de la semi diferencia de dos números

Lenguaje Algebraico

El lenguaje que usamos en operaciones aritméticas en las que sólo intervienen números se llama lenguaje numérico.
En ocasiones empleamos letras para representar cualquier número desconocido, realizamos operaciones aritméticas con ellas e, incluso, las incluimos en expresiones matemáticas para poder calcular su valor numérico.
El lenguaje que utiliza letras en combinación con números y signos, y, además, las trata como números en operaciones y propiedades, se llama lenguaje algebraico.
La parte de las Matemáticas que estudia la relación entre números, letras y signos se llama Álgebra.

Características del lenguaje algebraico

1.- El lenguaje algebraico es más preciso que el lenguaje numérico: podemos expresar enunciados de una forma más breve.
El conjunto de los múltiplos de 5 es 5 • = {±5, ±10, ±15, ...}.
En lenguaje algebraico se expresa 5 • n, con n un número entero.
2.- El lenguaje algebraico permite expresar relaciones y propiedades numéricas de carácter general.
La propiedad conmutativa del producto se expresa a • b = b • a, donde a y b son dos números cualesquiera.
3.- Con el lenguaje algebraico expresamos números desconocidos y realizamos operaciones aritméticas con ellos.
El doble de un número es seis se expresa 2 • x = 6

( VEASE FORMULARIO)

Algo Sencillo

Introducción al Álgebra

El Álgebra es muy divertida – ¡puedes resolver acertijos con ella!

Un Acertijo

¿Cuál es el número que falta?

-

2

=

4

Bueno pues, la respuesta es 6, ¿no? Porque 6-2=4.
Bien, en Álgebra no usamos espacios vacíos o cajas sino que usamos una letra (normalmente una x o una y, pero cualquier letra está bien). Entonces escribiríamos:

x

-

2

=

4

Es así de sencillo. La letra (en este caso una x) sólo quiere decir “aún no lo sabemos” y se la llama frecuentemente incógnita o variable.
Y una vez que la resuelves, escribes:

x

=

6

¿Por qué usar una letra?

	Porque:
	es más fácil escribir “x” que dibujar cajitas vacías (y más fácil decir “x” que “caja vacía”)
	si hubiera muchas cajitas vacías (muchas “incógnitas”) podríamos utilizar una letra diferente para cada una.

Cómo Resolver

El álgebra es como un acertijo donde empiezas con algo como “x-2=4” y quieres llegar a algo como “x=6”.
Pero en lugar de decir “obviamente x=6”, usa el siguiente método paso a paso:

• Piensa qué es lo que debes quitar para llegar a “x=…”
• Quítalo haciendo lo opuesto (sumar es opuesto a restar)
• Esto último hazlo en ambos lados

Aquí tienes un ejemplo:

Queremos quitar el “-2”	Para quitarlo, haz lo opuesto, en este caso suma 2	Hazlo en ambos lados:

Lo cual es ...	¡Resuelto!

¿Por qué agregamos 2 a ambos lados?

Para “mantener el equilibrio”…

	Agrega 2 a la izquierda	Agrega 2 a la derecha también
Equilibrada	¡Desequilibrada!	Equilibrada de nuevo

Acuérdate de esto:
Para mantener el equilibrio, ¡lo que se hace a un lado del “=”
también debe hacerse al otro lado!